Odds Of Hitting Poker Hands
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
- Texas Hold'em Poker Runner-Runner (Backdoor) Odds. When it takes two perfect cards on both the turn and the river to covert an average or weak hand after the flop to a strong one, this should normally qualify as a 'long shot'. Also, 'strong' hands are considered here to be straights and better.
- You have 15 outs so the odds of hitting one of your draws on the turn are 2.13 to 1. The pot is offering 5 to 1 odds, so you shouldn’t fold. Your odds of hitting one of your draws by the end of the hand is.85 to 1, which makes you a favorite to win the hand. You should raise because you’ll win the hand more often than you’ll lose at this.
- Poker Odds Of Hitting Over Cards While Having A Pair As you see from the table, you should not be surprised to see over cards even when holding premium pairs. The probability of that happening is reasonably high and you will see and over card to pocket jack on the flop around 57% of the time.
- The Odds of Making a Straight in Poker The odds of flopping a Straight with a premium connector is 1.29% or 1 in 77.5 Definition of Straight – A Straight is formed with 5 cards all of consecutive rank.
___________________________________________________________________________
Preliminary Calculation
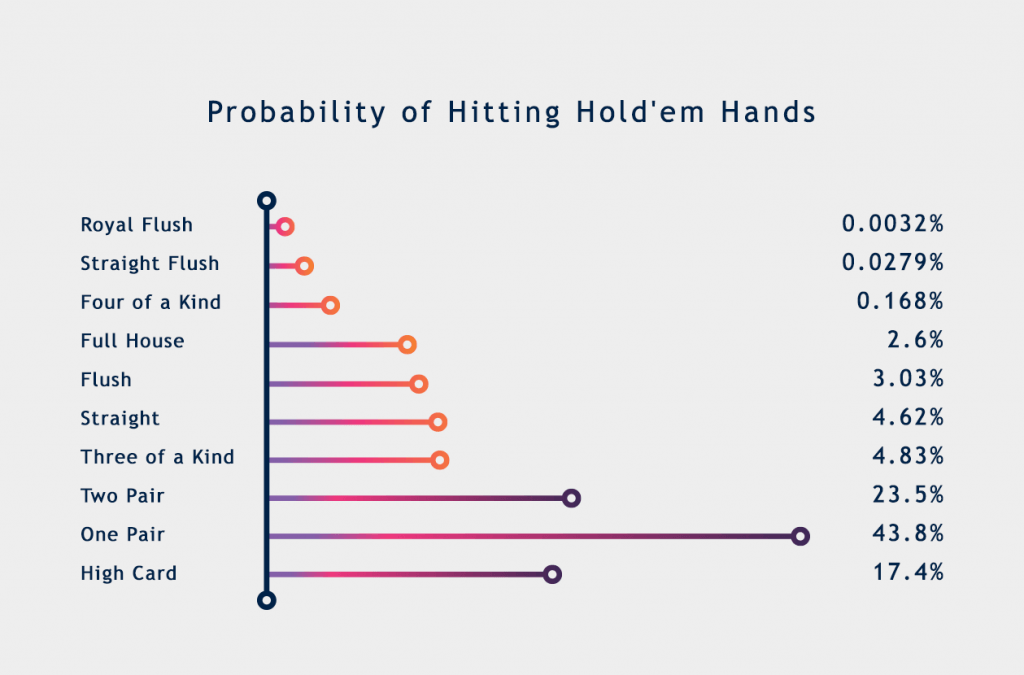
What are the odds of me hitting. Based on the probability of how many ways particular hands that can be dealt at a table with seven cards from a 52 card deck, the way that you want to play your combinations is to achieve the higher ranking hands where probabilities aren't out of the range of 'realistic'.
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced “n choose r”, which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of “3 diamond, 2 heart” hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
Here’s a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let’s fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2’s and choosing 2 cards out of the four 8’s. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
High Card
The count is the complement that makes up 2,598,960.
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
___________________________________________________________________________
2017 – Dan Ma
Poker odds can appear confusing at first, but once you understand some of the basic fundamentals about how they work, not only will you have a much better understanding of the game itself, but you’ll also stand a higher chance of winning while playing the game.
In this post, we’re going to take a look at all forms of poker odds, from poker hand odds, how to calculate poker odds, the best poker winning hands, and more – and we’ll begin by taking a look at how exactly the odds work in conjunction with the game.
How Poker Odds Work
To look at how poker odds actually work, it can be handy to use an example of a football game. Let’s say the Chargers are playing the Eagles. A bookmaker may give the Eagles 3:1 odds to beat the Chargers. This means that for every $1 you staked, you would win $3, were the Eagles to win.
This, of course, roughly equates to the Eagles having a 1 in 3 chance of beating the Chargers – and this is the general ethos of how odds work, both in sports betting, and poker.
The higher the odds, the less chance you have of winning – and subsequently, the lower the odds, the more chance you have of winning.
Poker Hand Odds
One of the most common scenarios you’ll hear about odds in poker, is when looking at your “outs”. We’ll cover this in the section below – in this part of the guide, we’re going to look at the actual odds of getting some of the most popular and sought-after poker hands.
- Being Dealt Pocket Aces: Pocket aces are the premium starting hand in ALL Texas Hold’em games, and the odds of being dealt two aces is 0.4525% – equating to odds of 1:220. This means that you can expect to be dealt pocket aces once out of every 220 hands you play. (An interesting statistic is the chances of both you AND your opponent being dealt pocket aces. In this situation, the probability is just 0.0816%, equating to odds of 1:1,224!
- Hitting a Set on The Flop: Most players will always try to reach the flop when they hold a pair in their hand, pre-flop, as, if they’re able to make a 3-of-a-kind hand, they stand a very good chance of winning against their opponents. If you hold a pair pre-flop, the chances of hitting a set on the flop are relatively good; the probability is 11.7551%, equating to odds of 1:8.
- Hitting Quads: 4-of-a-kind is one of the strongest hands in Texas Hold’em, and it’s a hand that – despite being very hard to get – probability wise, isn’t actually too hard! The probability of making quads if you have a pair pre-flop, and make it all the way to the river, is 0.8163%, equating to odds of 1:122. Things become a little crazier when you look at the chances of two players hitting quads; in this case, the probability is just 0.0003%, equating to odds of 1:312,663!
- Royal Flush: The unbeatable hand – the hand all players dream of getting – a Royal Flush is the best possible hand in Texas Hold ‘Em poker, and cannot be beaten. Interesting, the board will only allow for a Royal Flush 1 in 59 times – and the odds of just ONE player making a royal flush at a full 9-person ring game is 1:3,628.
That’s just a few of the most common poker odds scenarios. It can be useful to have a rough idea of the odds for various hands and occurrences – but for the most-part, you don’t need to think into it too deeply, as the more important thing to worry about is the odds of you hitting your “outs”.
Outs and How to Use Them to Calculate Probability in Texas Hold’em
In Texas Hold’em poker, if you require an additional card, or more than one card to complete your hand, you’ll be looking to hit what’s known as an ‘out’.
For example, say you hold 5, 6 off-suit pre-flop, and the board comes King, 7, 8. You now have an up-and-down straight draw, meaning you need to hit either a 4 or a 9 to complete a straight – a strong hand that gives you a very good chance of winning over your opponents.
Now, in a 52-card deck, there are four 4’s, and four 9’s, which means you have 8 cards out of the 52 to hit your hand. However, you’ve already been dealt two cards – and there are three showing on the flop – which means the actual probability of hitting one of the cards you need is 8:47.
This means that approximately one in 6 times the turn card is dealt, you’ll hit your hand. Now, you may be thinking “why is this important” – and there are two reasons.
The first, is the simple fact that it’s good to know how likely you are to hit your hand. The second, and far more important reason, is that knowing how many outs you have allows you to make solid mathematical decisions, when faced with a bet. We’ll look at this in the following section.
Should You Call an Opponent’s Bet?
Using the example above, we can safely say that you’ll hit your hand – on average – once in every 6 times when the turn card is dealt.
Now, let’s say there is currently $40 in the pot, and your opponent bets $10. There are no other players in the hand.
In order to see a turn card, you must call $10. With the $40 in the pot, and the $10 your opponent bet, that means you’re required to risk $10, to have the potential to win $50. This means you’re getting 1:5 on your money – which means that over the long run, this would be a losing play, to call.
Now, say that there was $80 in the pot already, instead of $40. Now, when your opponent bets $10, you have to call $10 to have the chance of winning $90 – meaning you’re getting 1:9 on your money. In this scenario, it would almost always be a profitable decision to call, as, while you won’t always hit your hand, you’re getting odds that make it worthwhile, as over the long-run it would be a profitable, winning move.
That’s just one example, and of course, things become more complex when you start involving multiple players, and factoring in the possibility of re-raises. That being said, it should serve as a good starting-point for you to learn more about “outs”, and how they tie in with poker odds.
Tips to Improve Your Knowledge of Poker Odds
Like many things in life, having a firm grasp of poker odds and poker statistics takes time. There is no “quick-fire” way to memorize everything about odds, and how to use them in your game, and much of it comes from practice.
Thankfully, there are many great poker theory books available to purchase today, that you can use to improve your knowledge of the game and determine your odds of hitting your poker outs.
It’s worth pointing out that poker theory can become very complex – and even things like the poker outs example we looked at above can become difficult, when looking at things like reverse-implied odds.
As a general rule of thumb, the best thing to do is to simply stay calm while playing, and figure out how many cards you need to hit your hand. Calculate whether you’re getting the right pot odds to call to try and hit one of your poker outs – and don’t forget to factor in the fact that if there are multiple players to act after you, there’s a chance you may get raised and subsequently forced out of the hand.
Things to Remember
It’s important to note that many times, you’ll probably find that you simply don’t have time – or you forget – to work out the odds, especially when you’re in the middle of a hectic hand. However, try to brush up on your knowledge of poker winning hands from time to time, as you’ll find that this will soon become concreted within your brain, helping you to get a firm grasp on the game.
Frequently Asked Questions
Below, we’re going to finish this guide by answering a few commonly asked questions about poker odds.
How to Work Out Outs In Your Head
Like we just mentioned, there will often be times that it just seems too confusing, or hard to work out the odds in your head. When you find yourself in situations like these, one of the best pieces of advice we can offer, is to just slow down, take a deep breathe, and keep yourself calm and collected.
In most Texas Hold’em games, you’ll have ample time to think about the hand, and the odds – and if you’re looking for a quick way to work them out, it can help to brush up on some of the more common situations you’ll come across. For example, if you hold a pair pre-flop, and find yourself against a player holding two over cards, there is pretty much a 50/50 chance of you winning the hand.
Things like this can help – but above and beyond, it all comes down to practice as we keep mentioning, so spend a few minutes every day reading about poker statistics, and you’ll soon find that it becomes second nature to you!
What Are Outs?
The “outs” are the cards that you can hit to complete your hand. Say, for example, that you hold 2 cards that are suited hearts, and the flop contains another two cards that are hearts, and one spade. You “outs” are the remaining heart cards in the deck that can be drawn on the turn or the river, to help you complete your hand.
How to Count Outs
Odds Of Hitting Poker Hands Game
To determine how many outs you have, you simply need to work out how many cards there are in the deck that help you to complete your hand – and then minus the two hole cards you’ve been dealt, and the community cards currently visible.
Odds of Winning Poker
Some of the most common poker hands that you’d want to know the odds of, include an open-ended straight draw, which has odds of approximately 6/1, four-to-a-flush, which offers odds of around 4/1, an inside straight draw, which is approximately 10/1, and having a pair pre-flop which then turns into a set when the community cards are dealt, which is approximately 8/1.
Odds Of Hitting Poker Hands Signals
Odds of Being Dealt Poker Aces
The odds of being dealt pocket aces in a standard Texas Hold’em game is around 220/1. This means that every 220 hands you play, you can expect to see pocket aces once – although, as is the case with ANY type of gambling, it could be 2,000 hands before you see aces… or you may see them back-to-back. It’s all a game of chance at the end of the day.
Chances of Winning with Pocket Aces
Pocket aces are – by far – the strongest starting hand in Texas Hold’em, and the chances of you winning with them largely depends on how many players are also in the hand with you. As a general rule of thumb, if you hold pocket aces on a 9-player table, you have odds of around 25% to win the hand at showdown – but the odds of you winning improve as more players drop out of the hand, so it can often be a good idea to play aces aggressively to avoid too many players joining the hand.
Odds Of Hitting Poker Hands In Golf
- Tags: